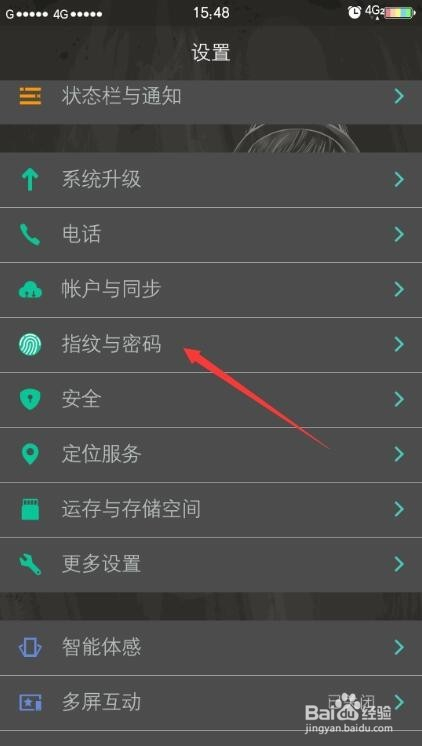
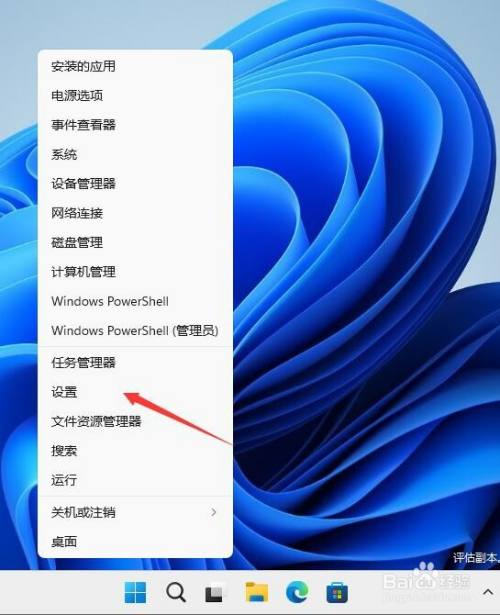
上图中的场景在战争片中经常可以看到,一般做出这样的动作,接下来就是一阵狠恶的炮击,并且可以切确的冲击到方针物。
而一般利用这种方式就是为了测量方针物的距离,所利用的进犯兵器为迫击炮,一种可以或许发射弧线炮弹的兵器。
一般迫击炮的发射炮弹的初始速度是一样,所以可以经由过程调节迫击炮的发射角度,就可以精确的知道炮弹的落点。
这个出厂的时辰就已经计较好了,什么样的角度能打到多远的距离,都有具体申明。
那么方针的物体的距离呢?这就需要在实战中按照具体的环境进行测量。
而我们在战争片中看到的伸个拇指就是在测量方针物的距离,这种方式称为眼跳法测距,其实根基道理跟我们天文学上最根基的视差法是一样的。
这个方式可以或许测距的原因是,我们有两只眼睛,而且它们之间有必然的距离,还有一点就是光线沿着直线传布。
此刻您身处您伸出您的手臂,而且竖起拇指,放在您面前的任何位置,然后轮流闭上摆布眼睛,您就会看到拇指的位置会落在远处参考物分歧的位置上。
这种摆布眼看到物体位置的分歧,就是我们所说的视差,而测距恰是依靠视差来进行的。接下来我们就说下拇指测距的道理。
若是您是一个迫击炮手,此刻要精确的冲击到远处的方针物,那么您就要知道方针物和您的距离,然后按照这个距离调节迫击炮的角度。
接到号令今后,您只需要伸出您的右臂,然后竖起大拇指,但这是您不克不及把大拇指放在面前的任何位置的,而是要让您的拇指和右眼连结在一条直线上,而且和方针物对齐。
这个很简单,光线沿直线传布,两点一线您很轻易可以或许对齐。就像上图那样,右眼、拇指、方针。
对齐今后手臂不要动,连结不变,此刻闭上右眼,展开左眼,您就会看到手指落在了其他位置上。就像上图中的左眼、拇指和远处的任何参照物。
完当作以上的操作,您就刹时在空间中构建起了两个相似三角形。
求解这个三角形的任何边长角度,都是简单的几何常识了,初中就可以完当作。上图就可以看到其实我们要知道的是Y的距离。也就是您和方针的距离,再精确一点就是再加上您手臂的距离。
上图中两个相似三角形顶角是相等的,所以我们就能写出X/Y=A/B。
那么Y=XB/A。此中A就是您瞳孔之间的距离,B就是您手臂的距离,X就是视差偏移的距离,此中A、B这两个量是已知的,作为一个优异的炮手,您早就对您的身体的参数洞若观火。
若是您是个新手,身段与大部门人八两半斤,您也可以操纵大大都人的参数,B/A大约等于10。
最难的处所就是您如何确定X,这就是一个优异炮手和一个垃圾炮手的区别地点了。
若是您要进犯别人的一辆坦克,拇指瞄准坦克的头部,然后左眼看见拇指偏移到了布景的右边,坦克的长度是已知的,那么您就应该按照经验估算出偏移的距离可以或许放几个坦克,而且知道偏移量X是几多。
若是您要进犯仇敌的碉堡,首先应该把握仇敌碉堡的尺寸,然后把拇指瞄准碉堡的一个遍,展开左眼,就会看到拇指偏移,然后按照碉堡的尺寸进而估量出偏离的距离。
这就是要您拥有丰硕的实战经验,可是对于一个内行来说,就是刹时完当作的事。很是简单。
那么天文学上的视差法如何测量星星的距离呢?
和迫击炮手的道理不异,但方式分歧。
视差法有个特点,就是拇指距离您双眼越近,那么您瓜代双眼不雅察拇指的时辰,拇指相对于远处固定的布景偏移的量就越大。
此刻您伸出手臂,这回伸出一半,试着看下拇指,然后再把手臂伸直再看,您就会发现区别。
那么如果我们看很是遥远的一个树木、山头呢?您就会发现,就算您瓜代双眼,已经很难分辩出两者之间位置的误差了。
这是因为这些物体离您太远,也是因为您的两个瞳孔之间的距离太近了。所以您想要在原地站着测量天体的距离是不成能的了。
例如操纵视差法测量月球的距离,就要在两个相隔数千公里的处所,别离不雅察月球,然后测量出月球相对于恒星布景在天空中偏移的距离。按照这个距离在天空中所占的角度大小,就能知道此次测量的视差角。
我们知道了等腰三角形的顶角,知道了它的底边长度,很轻易就能算出月球距我们的距离。
月球还相对较近一些,可是想要测量遥远的恒星,就算是把地球的直径看成基线,也很难看出某一刻横标的目的相对于整个恒星布景的偏移,那怎么办?
我们把地球绕太阳的轨道直径看成了基线,首先在1月份的时辰某一个特定的时候不雅察方针恒星的位置,然后再六月份地球转到绕太阳轨道另一边的时辰,再在统一时候测量这颗恒星再天空中的位置。
按照这个位置的误差我们就能知道以地球轨道直径为底边的等腰三角形的顶角是几多,然后简单的三角函数算出这颗恒星距我们的距离。
很是简单,这种方式的局限性很是大,因为地球的轨道直径是我们可以或许用到最长的基线了。所以这种方式测量恒星距离的规模很是有限,一般就能测个银河系内的恒星和天体。
此刻我们已经很罕用视差法测量天体的距离了,并且在加倍遥远的处所我们可以经由过程变星的周光关系、超新星等一系列方式可以测算出数百亿光年的距离。
可是简单的几何干系,在人类汗青上的测距问题上阐扬了重大的进献,在汗青上人类初次的天体、天文测距使命都是经由过程几何方式算出来的。
例如公元前3宿世纪的埃拉托色尼就操纵几何经由过程定量的方式知道了地球是个球,而且算出了地球的周长;
也在统一期间,古希腊学者阿里斯塔克斯经由过程简单的几何初次为人类算出了月球以及太阳的距离,固然禁绝确,但也算得上是一次科学史上的豪举。
小小的拇指测距,小小的迫击炮发射前的动作,其实也包含着深刻的科学。它也是天文学成长的根本。